什么是分层图？

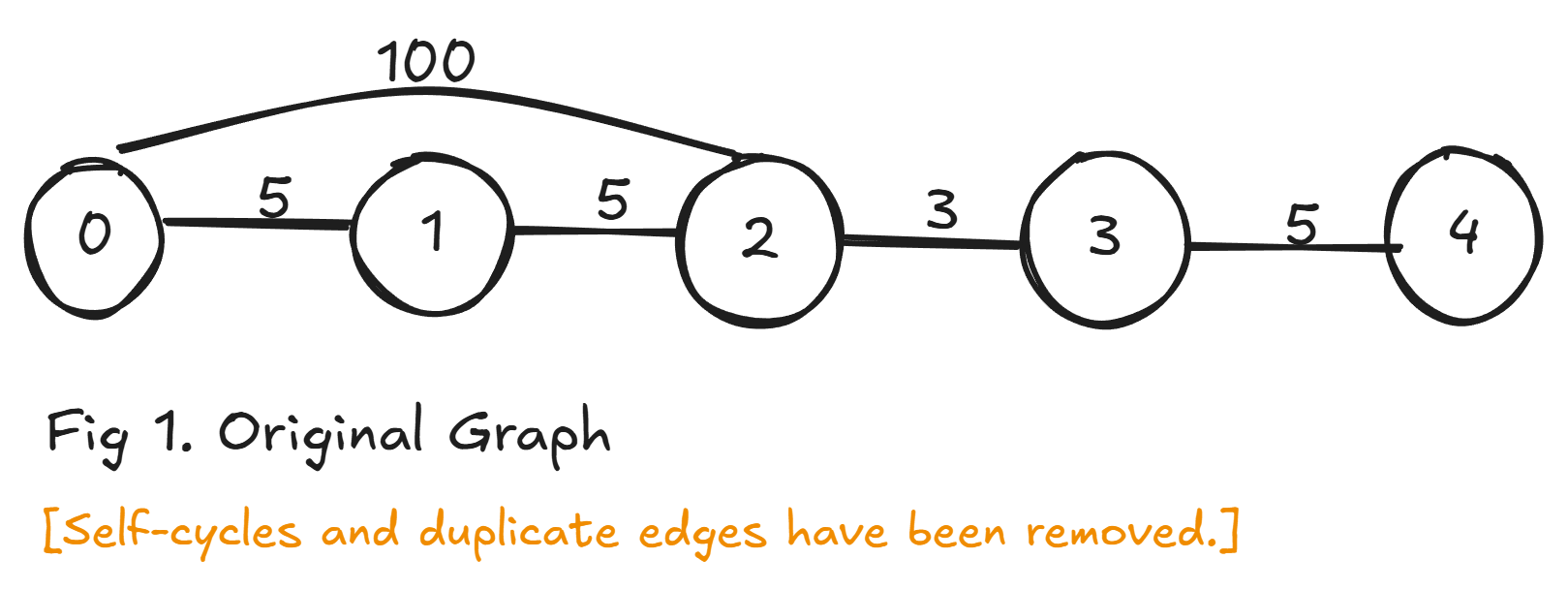
所谓分层图，即通过构建一张新图使得一张图有多个维度。一个典型的例子是使一张图复制出一份或多份，并在复制出的不同的层之间根据要求连接某些点。

一个典型的应用就是在不同路径上有 $k$ 个决策 $p_1,p_2,p_3$ ，那么对于每个决策 $p_i$ ，我们构建一层新的图使得边 $E(u,v)$ 可以用来表示决策 $p_i$ 。后续的操作经常使用最短路/最长路相关算法求解。

例题

P4568 [JLOI2011] 飞行路线

题目概述

给定一个包含 $n$ 个节点和 $m$ 条边的带权无向图 $G$ （节点由 $0 \sim n - 1$ 编号）和 $k$ 次决策（$0 \leq k \leq 10$），对于每个决策 $D_i$ ，可以以 $0$ 为边权通过任意一条边一次。求从节点 $s$ 到 $t$ 的最小花费。

分析

容易发现在不考虑进行决策的情况下（即 $k=0$ 时），题目转化为求无向图上的最短路径。显然可以通过 Dijkstra 等算法在 $O(m \log m)$ 时间内解决。

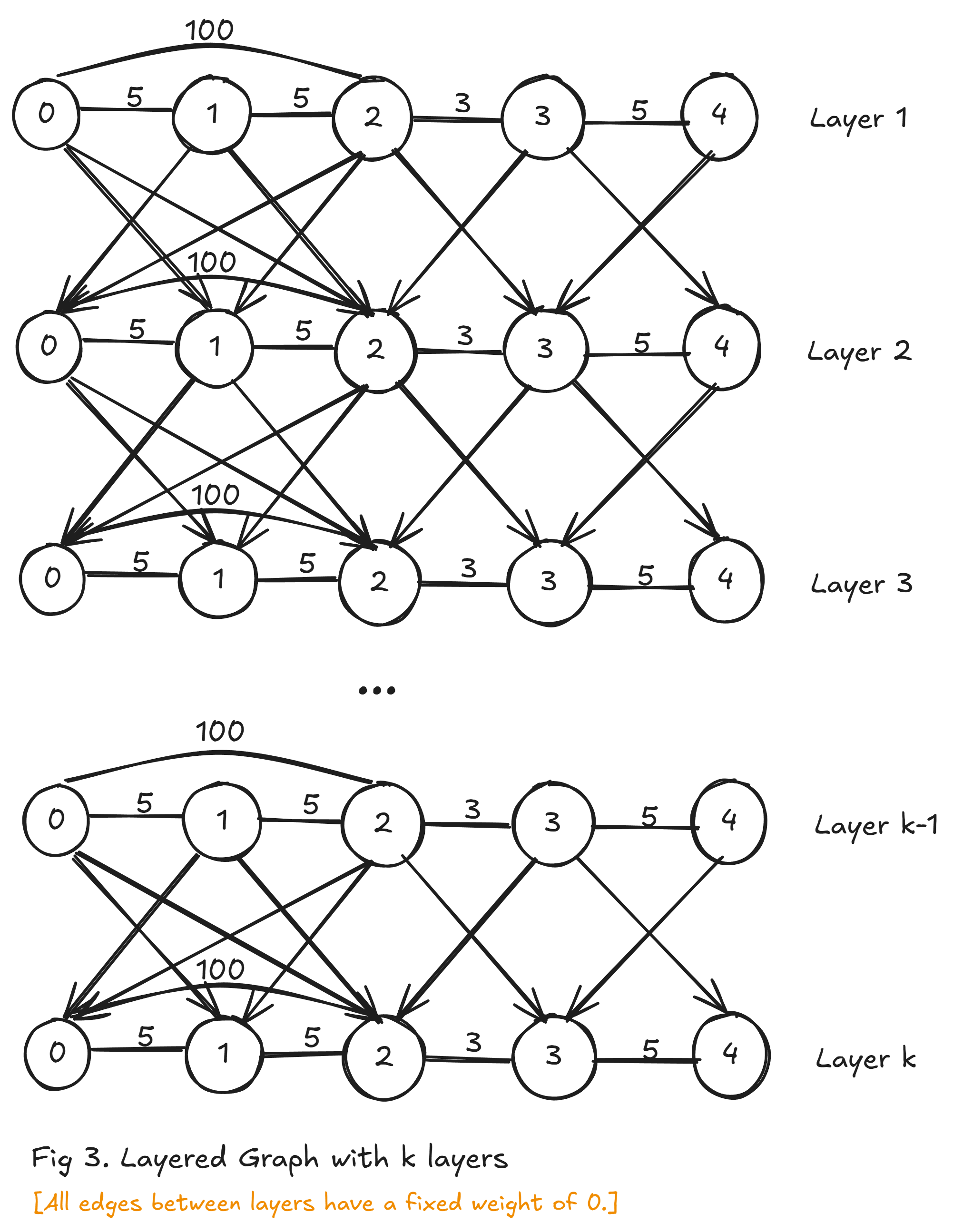
考虑进行决策。对于每一条边，我们都可以有选择按照原有边权走或者按边权为 $0$ 走两种选择。显然后者只能选择最多 $k$ 次（不一定要全选完 $k$ 次）。那么，我们不妨对于每条边 $E(u,v,w)$ 增设一个决策边 $E'(u,v,0)$ ，即选择走边 $E'$ 意味在边 $E$ 上进行一次决策。

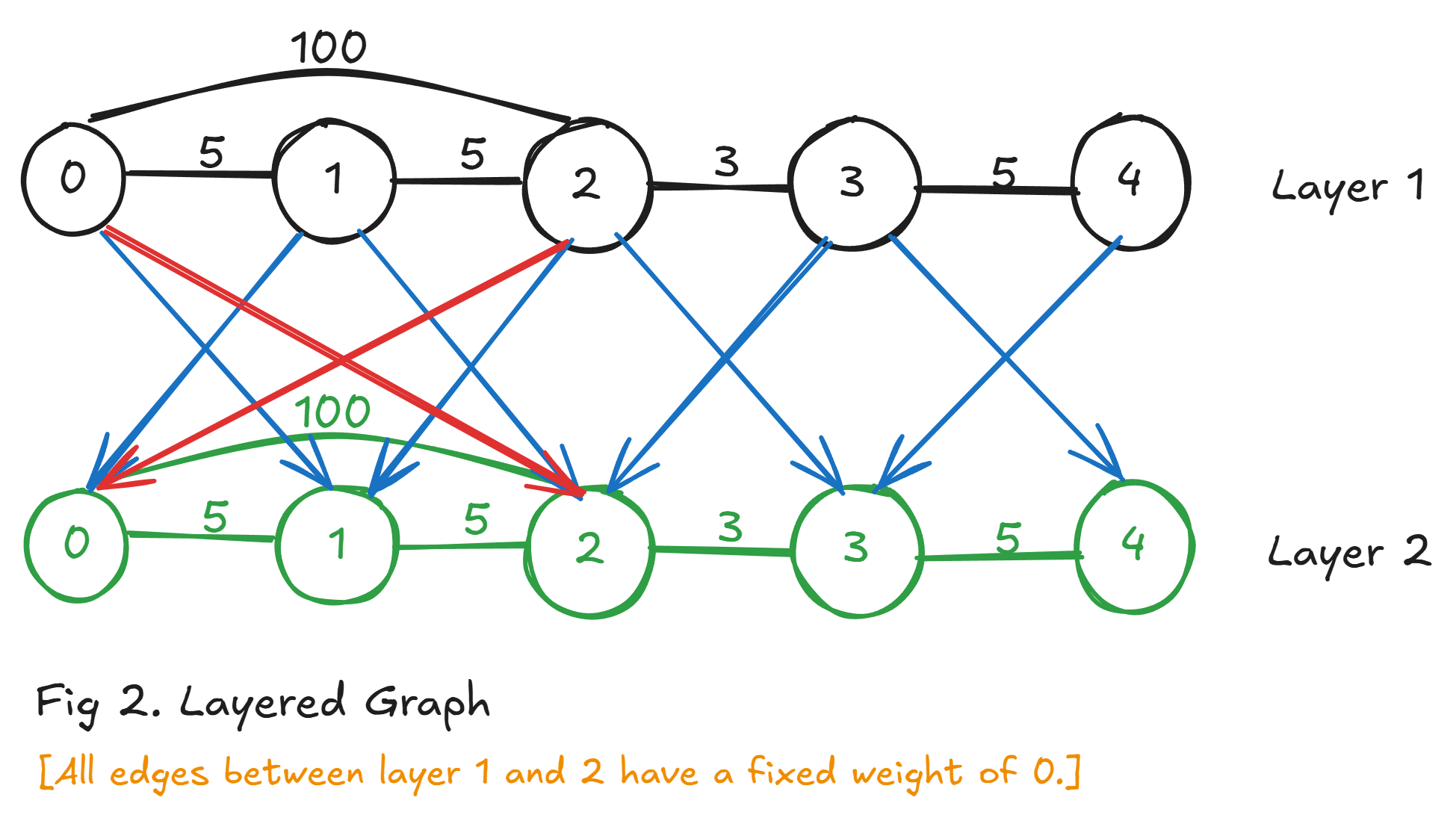
接下来我们需要考虑限定 $k$ 次决策。容易发现，在上图中，我们在下层新建了 $n$ 个节点 $V_0' \sim V_1'$ ，并将决策边的终点设在了第二层对应点上。这样，对于每一次决策，我们都可以保证单向性（上层的点只能到达下层）。同时，因为每一层的节点之间都有来自原始图的连边，所以不会影响正常边的统计。

显然，对于 $k$ 次决策，我们只需要建立 $k$ 层上述的图即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

int n, m, K, s, t;

struct Edge {
    int v, w;
};
vector<Edge> G[N];
int dis[N], vis[N];

void addEdge(int u, int v, int w) {
    G[u].push_back(Edge{v, w});
}

void dijkstra(int u) {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    struct Node {
        int dis, u;

        bool operator>(const Node& a) const {
            return dis > a.dis;
        }
    };
    priority_queue<Node, vector<Node>, greater<Node>> q;
    q.push(Node{0, u});
    dis[u] = 0;
    while (!q.empty()) {
        Node curr = q.top();
        q.pop();
        int u = curr.u;
        if (vis[u]) continue;
        vis[u] = 1;
        for (auto edge : G[u]) {
            int v = edge.v, w = edge.w;
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                q.push(Node{dis[v], v});
            }
        }
    }
}

int main() {
    for (int i = 0; i < N; i++) G[i].clear();
    scanf("%d%d%d", &n, &m, &K);
    scanf("%d%d", &s, &t);
    s++, t++;
    for (int i = 1; i <= m; i++) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        u++, v++;
        addEdge(u, v, w);
        addEdge(v, u, w);
        for (int i = 1; i <= K; i++) {
            int uu = i * n + u, vv = i * n + v;
            addEdge(uu, vv, w);
            addEdge(vv, uu, w);
            addEdge((i - 1) * n + u, vv, 0);
            addEdge((i - 1) * n + v, uu, 0);
        }
    }
    dijkstra(s);
    int ans = 0x3f3f3f3f;
    for (int i = 0; i <= K; i++) {
        ans = min(ans, dis[i * n + t]);
    }
    printf("%d\n", ans);
    return 0;
}

需要注意的是，在统计答案时我们需要在 $k$ 层中取最小值，因为不一定需要 $k$ 次决策才能到达终点。

P3119 [USACO15JAN] Grass Cownoisseur G

题目概述

给定一个 $n$ 个点 $m$ 条边的有向图 $G$ 和 $1$ 次决策，求从 $1$ 号节点返回到 $1$ 号节点的最长路。

定义一次决策为将任意一条边 $E(u,v)$ 变为 $E'(v, u)$ 。

分析

考虑建图。显然可以将决策转化为分层图求解。

对于原图 $G$ ，我们新建一个图 $G'$ 使得 $G'=G$ 。然后，我们对于 $E(u,v) \in G$ ，$E'(u',v') \in G'$ 间建立有向边 $E''(v, u')$ ，即对于原图和复制图中的每个点之间建立反向边。

然后可以考虑求最长路。显然上述做法建出来的图无法保证是 DAG ，故先进行 Tarjan 缩点后重新建带权图，最后使用拓扑排序求最长路。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

int n, m;
int dfn[N], low[N], color[N], sccCnt = 0, idx = 0, vis[N];
set<int> scc[N];
stack<int> s;
int dis[N], inDegree[N];

class Graph {
  private:
    vector<int> G[N];

  public:
    int inDegree[N];

    void addEdge(int u, int v) {
        G[u].push_back(v);
        inDegree[v]++;
    }

    vector<int> operator[](int x) {
        return G[x];
    }
} G, G2;

void tarjan(int u) {
    dfn[u] = low[u] = ++idx;
    vis[u] = 1;
    s.push(u);
    for (auto v : G[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (vis[v]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (dfn[u] == low[u]) {
        sccCnt++;
        while (!s.empty()) {
            int x = s.top();
            s.pop();
            scc[sccCnt].insert(x);
            color[x] = sccCnt;
            vis[x] = 0;
            if (u == x) break;
        }
    }
}

void toposort(int s) {
    queue<int> q;
    for (int i = 1; i <= sccCnt; i++) {
        if (G2.inDegree[i] == 0) q.push(i);
    }
    dis[s] = 0;
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (auto v : G2[u]) {
            G2.inDegree[v]--;
            if (G2.inDegree[v] == 0) {
                q.push(v);
            }
            if (dis[u] >= 0) dis[v] = max(dis[v], dis[u] + (int)scc[v].size());
        }
    }
}

int main() {
    memset(dis, -0x3f, sizeof(dis));
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++) {
        int u, v;
        scanf("%d%d", &u, &v);
        G.addEdge(u, v);
        G.addEdge(v, u + n);
        G.addEdge(u + n, v + n);
    }
    for (int i = 1; i <= 2 * n; i++) {
        if (!dfn[i]) tarjan(i);
    }
    for (int u = 1; u <= 2 * n; u++) {
        for (auto v : G[u]) {
            if (color[u] == color[v]) continue;
            G2.addEdge(color[u], color[v]);
        }
    }
    toposort(color[1]);
    printf("%d\n", max(dis[color[1]], dis[color[1 + n]]));
    return 0;
}

总结

分层图是一种实用的建图思想，可以解决多种图上决策问题。实际使用中需要注意层与层之间的联系，必要时可结合 Tarjan 缩点后处理。